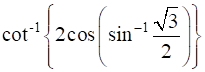
For finding the solution we first of need to find the principal value of

Sin^–1

Let,

Sin^–1 =y

⇒ sin y =

⇒ sin

The range of principal value of sin^–1 is and sin

Therefore, the principal value of Sin^–1 is

∴ The above equation changes to cot^–1(2cos)

Now we need to find the value of 2cos

∴ cos

⇒ 2cos = 1 x

⇒ 2cos = 1

Now the equation simplification to cot^–1(1)

Let cot^–1(1) = y

⇒ cot y = 1

= cot = 1

The range of principal value of cot^–1is (0, π)

and cot = 1

∴ The principal value of cot^–1(2cos(Sin^–1)) is