Evaluate each of the following:

RD Sharma - Mathematics (Volume 1)

Book: RD Sharma - Mathematics (Volume 1)

Chapter: 4. Inverse Trigonometric Functions

Subject: Maths - Class 12^th

Q. No. 1 of Exercise 4.7

Listen NCERT Audio Books - Kitabein Ab Bolengi

1

Evaluate each of the following:

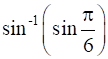
The value of sin is

∴ The question becomes sin^–1

Let sin^–1 ⁼ y

⇒ sin y =

= sin

The range of principal value of sin^–1 is and sin

Therefore, the value of sin^–1(sin) is .

Alternate Solution:

sin^–1(sin x) = x

Provided x ϵ

∴ we can write sin^–1(sin) =

1

Chapter Exercises

Exercise 4.1

Exercise 4.2

Exercise 4.3

Exercise 4.4

Exercise 4.5

Exercise 4.6

Exercise 4.7

Exercise 4.8

Exercise 4.9

Exercise 4.10

Exercise 4.11

Exercise 4.12

Exercise 4.13

Exercise 4.14

Very short answer

MCQ

1

Evaluate each of the following:

1

Evaluate each of the following:

1

Evaluate each of the following:

1

Evaluate each of the following:

1

Evaluate each of the following:

1

Evaluate each of the following:

1

Evaluate each of the following:
sin^–1(sin3)

1

Evaluate each of the following:
sin^–1(sin4)

1

Evaluate each of the following:
sin^–1 (sin12)

1

Evaluate each of the following:
sin^–1 (sin 2)

2

Evaluate each of the following:

2

Evaluate each of the following:

2

Evaluate each of the following:

2

Evaluate each of the following:

2

Evaluate each of the following:
cos^–1(cos 3)

2

Evaluate each of the following:
cos^–1(cos 4)

2

Evaluate each of the following:
cos^–1(cos 5)

2

Evaluate each of the following:
cos^–1(cos 12)

3

Evaluate each of the following:

3

Evaluate each of the following:

3

Evaluate each of the following:

3

Evaluate each of the following:

3

Evaluate each of the following:
tan^–1 (tan 1)

3

Evaluate each of the following:
tan^–1 (tan 2)

3

Evaluate each of the following:
tan^–1 (tan 4)

3

Evaluate each of the following:
tan^–1 (tan 12)

4

Evaluate each of the following:

4

Evaluate each of the following:

4

Evaluate each of the following:

4

Evaluate each of the following:

4

Evaluate each of the following:

4

Evaluate each of the following:

4

Evaluate each of the following:

4

Evaluate each of the following:

5

Evaluate each of the following:

5

Evaluate each of the following:

5

Evaluate each of the following:

5

Evaluate each of the following:

5

Evaluate each of the following:

5

Evaluate each of the following:

6

Evaluate each of the following:

6

Evaluate each of the following:

6

Evaluate each of the following:

6

Evaluate each of the following:

6

Evaluate each of the following:

6

Evaluate each of the following:

7

Write each of the following in the simplest form:

7

Write each of the following in the simplest form:

7

Write each of the following in the simplest form:

7

Write each of the following in the simplest form:

7

Write each of the following in the simplest form:

7

Write each of the following in the simplest form:

7

Write each of the following in the simplest form:

7

Write each of the following in the simplest form:

7

Write each of the following in the simplest form:

7

Write each of the following in the simplest form: