RD Sharma - Mathematics (Volume 1)

Book: RD Sharma - Mathematics (Volume 1)

Chapter: 4. Inverse Trigonometric Functions

Subject: Maths - Class 12th

Q. No. 6 of Exercise 4.7

Listen NCERT Audio Books to boost your productivity and retention power by 2X.

6

Evaluate each of the following:

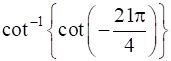
cot(–θ) is –cot(θ)


∴ The equation given above becomes cot–1(–cot)


cot = 1.


⇒ –cot = –1.


∴ we get cot–1(–1)


Let cot–1(–1) = y


⇒ cot y = –1


= – cot = 1


= cot


= cot


The range of principal value of cot–1is (0, π)


and cot = –1


∴ The value of cot–1(cot) is .


Chapter Exercises

Exercise 4.1
Exercise 4.2
Exercise 4.3
Exercise 4.4
Exercise 4.5
Exercise 4.6
Exercise 4.7
Exercise 4.8
Exercise 4.9
Exercise 4.10
Exercise 4.11
Exercise 4.12
Exercise 4.13
Exercise 4.14
Very short answer
MCQ

More Exercise Questions

1

Evaluate each of the following:
1

Evaluate each of the following:
1

Evaluate each of the following:
1

Evaluate each of the following:
1

Evaluate each of the following:
1

Evaluate each of the following:
1

Evaluate each of the following:

sin–1(sin3)
1

Evaluate each of the following:

sin–1(sin4)
1

Evaluate each of the following:

sin–1 (sin12)
1

Evaluate each of the following:

sin–1 (sin 2)
2

Evaluate each of the following:
2

Evaluate each of the following:
2

Evaluate each of the following:
2

Evaluate each of the following:
2

Evaluate each of the following:

cos–1(cos 3)
2

Evaluate each of the following:

cos–1(cos 4)
2

Evaluate each of the following:

cos–1(cos 5)
2

Evaluate each of the following:

cos–1(cos 12)
3

Evaluate each of the following:
3

Evaluate each of the following:
3

Evaluate each of the following:
3

Evaluate each of the following:
3

Evaluate each of the following:

tan–1 (tan 1)
3

Evaluate each of the following:

tan–1 (tan 2)
3

Evaluate each of the following:

tan–1 (tan 4)
3

Evaluate each of the following:

tan–1 (tan 12)
4

Evaluate each of the following:
4

Evaluate each of the following:
4

Evaluate each of the following:
4

Evaluate each of the following:
4

Evaluate each of the following:
4

Evaluate each of the following:
4

Evaluate each of the following:
4

Evaluate each of the following:
5

Evaluate each of the following:
5

Evaluate each of the following:
5

Evaluate each of the following:
5

Evaluate each of the following:
5

Evaluate each of the following:
5

Evaluate each of the following:
6

Evaluate each of the following:
6

Evaluate each of the following:
6

Evaluate each of the following:
6

Evaluate each of the following:
6

Evaluate each of the following:
6

Evaluate each of the following:
7

Write each of the following in the simplest form:
7

Write each of the following in the simplest form:
7

Write each of the following in the simplest form:
7

Write each of the following in the simplest form:
7

Write each of the following in the simplest form:
7

Write each of the following in the simplest form:
7

Write each of the following in the simplest form:
7

Write each of the following in the simplest form:
7

Write each of the following in the simplest form:
7

Write each of the following in the simplest form:

Students Store