Book: RD Sharma - Mathematics (Volume 1)
Chapter: 4. Inverse Trigonometric Functions
Subject: Maths - Class 12th
Q. No. 7 of Exercise 4.7
Listen NCERT Audio Books - Kitabein Ab Bolengi
7
Write each of the following in the simplest form:
Put x = tanθ
⇒ θ = tan–1(x)
tan–1{tanθ +
}
= tan–1{tanθ +
}
= tan–1{tanθ +secθ }
= tan–1
= tan–1
Sinθ = 
,cosθ = 
= tan–1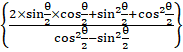
= tan–1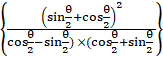
= tan–1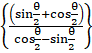
Dividing by 
we get,
= tan–1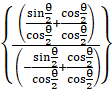
= tan–1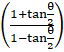
= tan–1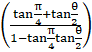
tan(x+y) = 
= tan–1
= 
From 1 we get
= 
.
Therefore, the simplification of given equation is 
.
