Write each of the following in the simplest form:
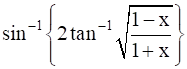
Put x = cos θ
= sin–1(2tan–1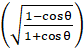
)
1 – cosθ = 2 sin2
and 1 + cos θ = 2 cos2
= sin–1(2tan–1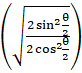
)
= sin–1(2tan–1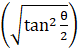
)
= sin–1(2tan–1(tan
))
= sin–1(
)
= sin–1(θ)
But θ = cos–1x
∴ The above expression becomes sin–1(cos–1x)
7