Given that,

Let us extend AD and PM up to point E and L respectively, such that AD = DE and PM = ML. Then, join B to E, C to

E, Q to L, and R to L

We know that medians divide opposite sides.

Hence, BD = DC and QM = MR

Also, AD = DE (By construction)

And, PM = ML (By construction)

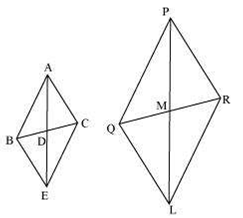
In quadrilateral ABEC,

Diagonals AE and BC bisect each other at point D.

Therefore,

Quadrilateral ABEC is a parallelogram.

AC = BE and AB = EC (Opposite sides of a parallelogram are equal)

Similarly, we can prove that quadrilateral PQLR is a parallelogram and PR = QL, PQ = LR

It was given in the question that,

ΔABE ΔPQL (By SSS similarity criterion)

We know that corresponding angles of similar triangles are equal

∠BAE = ∠QPL (i)

Similarly, it can be proved that

ΔAEC ΔPLR and

∠CAE = ∠RPL (ii)

Adding equation (i) and (ii), we obtain

∠BAE + ∠CAE = ∠QPL + ∠RPL

⇒∠CAB = ∠RPQ (iii)

In ΔABC and ΔPQR,

(Given)

∠CAB = ∠RPQ [Using equation (iii)]

ΔABC ΔPQR (By SAS similarity criterion)