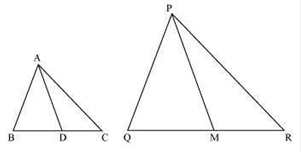
If AD and PM are medians of triangles ABC and PQR, respectively whereΔ ABC ~ Δ PQR, prove that![]()
It is given that ΔABC is similar to ΔPQR
We know that the corresponding sides of similar triangles are in proportion
![]() (i)
(i)
Also, ∠A = ∠P
∠B = ∠Q
∠C = ∠R (ii)
Since AD and PM are medians, they divide their opposite sides
BD = ![]() and,
and,
QM = ![]() (iii)
(iii)
From (i) and (iii), we get
![]() (iv)
(iv)
In ΔABD and ΔPQM,
∠B = ∠Q [Using (ii)]
![]() [Using (iv)]
[Using (iv)]
ΔABD ![]() ΔPQM (By SAS similarity)
ΔPQM (By SAS similarity)
![]()
37