Diagonals of a trapezium ABCD with AB || DC intersect each other at the point O. If AB = 2 CD, find the ratio of the areas of triangles AOB and COD
Since AB || CD,
∴∠OAB = ∠OCD and ∠OBA = ∠ODC (Alternate interior angles)

In ΔAOB and ΔCOD,
∠AOB = ∠COD (Vertically opposite angles)
∠OAB = ∠OCD (Alternate interior angles)
∠OBA = ∠ODC (Alternate interior angles)
ΔAOB ~ΔCOD (By AAA similarity)
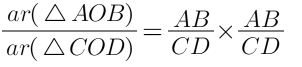
Since, AB = 2 CD
Therefore,


Therefore, the ratio of the areas of triangles AOB and COD is 4:1
5