Let, ∠MPR = x

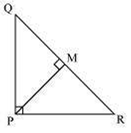
In triangle MPR,

∠MRP = 180^o – 90^o – x

∠MRP = 90^o – x

Similarly,

In triangle MPQ,

∠MPQ = 90^o - ∠MPR

∠MPQ = 90^o – x

In triangle QMP and PMR,

∠MPQ = ∠MRP

∠PMQ = ∠RMP

∠MQP = ∠MPR

Therefore,

ΔQMP ~ΔPMR (By Angle-Angle-Angle similarity)

PM² = QM×MR