In an equilateral triangle ABC, D is a point on side BC such that  Prove that 9AD 2  = 7AB 2

Question

In an equilateral triangle ABC, D is a point on side BC such that&#xA0; Prove that 9AD 2&#xA0; = 7AB 2

Philoid · Accepted Answer

Let the side of the equilateral triangle be a, and AE be the altitude of ΔABC

BE = EC =BC/2 = a/2

And, then, in ΔABE, we write,

AE²= AB²- BE²

or AE²= a²- a²/4

AE =

Given that, BD = 1/3 BC

BD = a/3

DE = BE – BD

= a/2 – a/3

= a/6

Applying Pythagoras theorem in ΔADE, we obtain

AD² = AE² + DE²

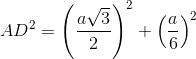
or

Now, a = AB or a² = AB²

or

or 36 AD²= 28 AB²

9 AD² = 7 AB²