Let ABC be a cone.

And,

A frustum DECB is cut by a plane parallel to its base

Now,

Let r1 and r2 be the radii of the ends of the frustum of the cone and h be the height of the frustum of the cone

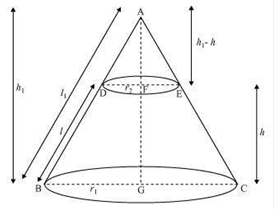
In ΔABG and ΔADF, DF||BG

= =

= =

= 1 - = 1 -

1 - =

= 1 – =

=

h1 =

Volume of frustum of cone = Volume of cone ABC - Volume of cone ADE

= r1²h1 - πr2² (h1 – h)

= [r1²h1 – r2² (h1 – h)]

= [r1² () – r2² ( - h)]

= [ - ]

= * h [ ]

= h []

= h [ r1² + r2² + r1r2]