Which of the following pairs of linear equations are consistent/inconsistent? If consistent, obtain the solution graphically:
(i) ![]()
(ii) ![]()
(iii) ![]()
(iv) ![]()
(i) We get,
= ![]()
=![]()
= ![]()
Hence,
= ![]()
Therefore these pair of lines have infinite number of solutions and ![]()
x + y = 5
x = 5 - y
putting y = 1,2,3 we get,
x = 5 -1 = 4
x = 5 - 2 = 3
x = 5 - 3 = 2
X | 4 | 3 | 2 |
Y | 1 | 2 | 3 |
And, 2x + 2y = 10
x = ![]()
X | 4 | 3 | 2 |
Y | 1 | 2 | 3 |
(ii) We get,
= ![]()
=![]()
= ![]()
Hence,
= ![]()
Therefore, these linear equations are parallel to each other and have no possible solution,
Hence, ![]()
(iii) We get,
= ![]()
=![]()
= ![]()
Hence,
= ![]()
Therefore, these linear equations are intersecting each other at one point and thus have only one possible solution.
Hence, ![]()
= ![]()
= ![]()
X | 0 | 1 | 2 |
Y | 6 | 4 | 2 |
And, ![]()
= ![]()
X | 1 | 2 | 3 |
Y | 0 | 2 | 4 |
Graphical representation
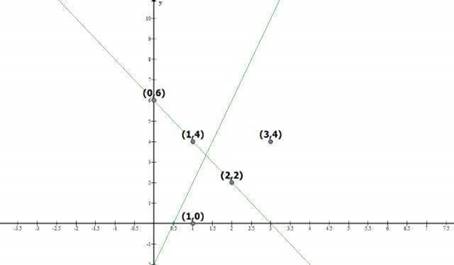
(iv) We get,
= ![]()
=![]()
= ![]() s
s
Hence,
= ![]()
Therefore, these linear equations are parallel to each other and have no possible solution,
Hence, ![]()