(i) Here, first term a = 3

Now,

The Common difference of the A.P. can be calculated as:

a₄ – a₃

= - 3 – ( -1)

= - 3 + 1

= - 2

a₃ – a₂

= - 1 – 1

= - 2

a₂ – a₁

= 1 – 3

= - 2

Now, herea_k+1 – a_k = - 2 for all values of k

Hence, first term = 3 and common difference = - 2

(ii) a₄ – a₃

= 7 – 3

= 4

a₃ – a₂

= 3 – (-1)

= 3 + 1

= 4

a₂ – a₁

= - 1 – (-5)

= - 1 + 5

= 5

Now, here, a_k+1 – a_k = - 2 for all values of k

Therefore, first term = - 5 and common difference = 4

(iii) From the question,

a₄ – a₃

=

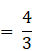
a₃ – a₂

=

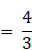
a₂ – a₁

=

Now, a_k+1 – a_k = - 2 for all values of k

Therefore,

First term = 1/3 and common difference = 4/3

(iv) a₄ – a₃

= 3.9 – 2.8

= 1.1

a₃ – a₂

= 2.8 – 1.7

= 1.1

a₂ – a₁

= 1.7 – 0.6

= 1.1

Now, here, a_k+1 – a_k = - 2 for all values of k

Therefore,

First term = 0.6 and common difference = 1.1