If 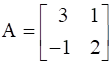 and
and 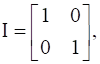 then find λ so that A2 = 5A + λI.
then find λ so that A2 = 5A + λI.
Given: ![]() ,
, ![]() and
and ![]()
Now, we will find the matrix for A2, we get
![]()
![]()
[as cij = ai1b1j + ai2b2j + … + ainbnj]
![]()
![]()
Now, we will find the matrix for 5A, we get
![]()
![]()
![]()
So,
![]()
Substitute corresponding values from eqn(i) and eqn(ii), we get
![]()
![]()
![]()
[as rij = aij + bij + cij]
And to satisfy the above condition of equality, the corresponding entries of the matrices should be equal,
Hence, ![]() and
and ![]()
So the value of λ so that ![]() is – 7
is – 7
28