(i) We know: In AP, middle term is average of the other two terms

Hence, middle term = (2 + 26)/2 = 28/2 = 14

Thus, above AP can be written as 2, 14, 26

(ii) The middle term between 13 and 3 will be;

(13 + 3)/2 = 16/2 = 8

Now, a₄ – a₃ = 3 – 8 = - 5

a₃ – a₂ = 8 – 13 = - 5

Thus, a₂ – a₁ = - 5

Or, 13 – a₁ = - 5

Or, a₁ = 13 + 5 = 18

Thus, above AP can be written as 18, 13, 8, 3

(iii) We have, a = 5 and a₄ = 91/2

Now common difference:

a₄ = a + 3d

= 5 +

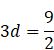
d =

Hence, using d, 2^nd term and 3^rd term can be calculated as:

a₂ = a + d

= 5 +

=

a₃ = a + 2d

= 5 +

= 8

Therefore, the A.P. can be written as:

5,

(iv) Here, a = - 4 and a₆ = 6

Common difference:

a₆ = a + 5d

6 = -4 + 5d

5d = 6 + 4 = 10

d = 2

The second, third, fourth and fifth terms of this AP are:

a₂ = a + d = - 4 + 2 = - 2

a₃ = a + 2d = - 4 + 4 = 0

a₄ = a + 3d = - 4 + 6 = 2

a₅ = a + 4d = - 4 + 8 = 4

Thus, the given AP can be written as: - 4, - 2, 0, 2, 4, 6

Let us take 38 as the first term and – 22 as the 5th term

Using this, common difference can be calculated as follows:

a₅ = a + 4d

= 38 + 4d

4d = - 22 – 38 = - 60

d = - 15

If 38 is the second term, then first term:

a = a₂ – d = 38 + 15 = 53

Third, fourth and fifth terms ar:

a₃ = a + 2d = 53 + 2(- 15) = 53 – 30 = 23

a₄ = a + 3d = 53 – 45 = 8

a₅ = a + 4d = 53 – 60 = - 7

So, the AP can be written as: 53, 38, 23, 8, - 7, - 22