If 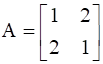 and f(x) = x2 – 2x – 3, show that f(A) = 0.
and f(x) = x2 – 2x – 3, show that f(A) = 0.
Given: ![]() and
and![]()
To show that ![]()
Substitute ![]() in
in ![]() , we get
, we get
![]()
I is identity matrix, so ![]()
Now, we will find the matrix for A2, we get
![]()
![]()
[as cij = ai1b1j + ai2b2j + … + ainbnj]
![]()
![]()
Now, we will find the matrix for 2A, we get
![]()
![]()
![]()
Substitute corresponding values from eqn(ii) and (iii) in eqn(i), we get
![]()
![]()
![]()
[as rij = aij + bij + cij],
![]()
So,
![]()
Hence Proved
37