For what value of k is the function 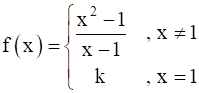 continuous at
continuous at
x = 1?
Ideas required to solve the problem:
1. Meaning of continuity of function – If we talk about a general meaning of continuity of a function f(x) , we can say that if we plot the coordinates (x , f(x)) and try to join all those points in the specified region, we can do so without picking our pen i.e you will put your pen/pencil on graph paper and you can draw the curve without any breakage.
Mathematically we define the same thing as given below:
A function f(x) is said to be continuous at x = c where c is x–coordinate of the point at which continuity is to be checked
If:–
![]() …… equation 1
…… equation 1
where h is a very small positive no (can assume h = 0.00000000001 like this )
It means :–
Limiting value of the left neighbourhood of x = c also called left hand limit LHL ![]() must be equal to limiting value of right neighbourhood of x= c called right hand limit RHL
must be equal to limiting value of right neighbourhood of x= c called right hand limit RHL ![]() and both must be equal to the value of f(x) at x=c f(c).
and both must be equal to the value of f(x) at x=c f(c).
Thus, it is the necessary condition for a function to be continuous
So, whenever we check continuity we try to check above equality if it holds true, function is continuous else it is discontinuous.
Given,
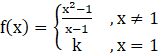 …… equation 2
…… equation 2
We need to find the value of k such that f(x) is continuous at x = 1
Since f(x) is continuous at x = 1
∴ (LHL as x tends to 1) = (RHL as x tends to 1) = f(1)
∴ ![]()
As, f(1) = k [from equation 2]
We can find either LHL or RHL to equate with f(1)
Let’s find RHL but if you want you can proceed with LHL also.
RHL = ![]()
= ![]()
As, f(x) is continuous
∴ RHL = f(1)
∴ k = 2