RD Sharma - Mathematics (Volume 1)

Book: RD Sharma - Mathematics (Volume 1)

Chapter: 9. Continuity

Subject: Maths - Class 12th

Q. No. 21 of Exercise 9.1

Listen NCERT Audio Books - Kitabein Ab Bolengi

21

Determine the value of the constant k so that the function 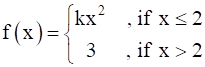is continuous at x = 2.

Given:


It is clear that when x<2 and x>2, the given function is continuous at x = 2.


So, at x = 2




= 4k



We know that,


If f is continuous at x = c, then The Left–hand limit, the Right–hand limit and the value of the function at x = c exist and are equal to each other.




⇒ 4k = 3


k =


Therefore, the required value of k is


21

Chapter Exercises

Exercise 9.1
Exercise 9.2
Very short answer
MCQ

More Exercise Questions

1

Test the continuity of the following function at the origin :
2

A function f(x) is defined as Show that f(x) is continuous at x = 3.
3

A function f(x) is defined as

Show that f(x) is continuous at x = 3.
4

If Find whether f(x) is continuous at x = 1.
5

If Find whether f(x) is continuous at x = 0.
6

If Find whether f is continuous at x = 0.
7

Let Show that f(x) is discontinuous at x = 0.
8

Show that is discontinuous at x = 0.
9

Show that is discontinuous at x = a.
10

Discuss the continuity of the following functions at the indicated point(s).

at x = 0
10

Discuss the continuity of the following functions at the indicated point(s).

at x = 0
10

Discuss the continuity of the following functions at the indicated point(s).

at
x = a
10

Discuss the continuity of the following functions at the indicated point(s).

at x = 0
10

Discuss the continuity of the following functions at the indicated point(s).

at x = 1
10

Discuss the continuity of the following functions at the indicated point(s).

at x = 1
10

Discuss the continuity of the following functions at the indicated point(s).

at x = 0
10

Discuss the continuity of the following functions at the indicated point(s).

at x = a
11

Show that is discontinuous at x = 1.
12

Show that is continuous at x = 0
13

Find the value of ‘a’ for which the function f defined by is continuous at x = 0.
14

Examine the continuity of the function at x = 0. Also sketch the graph of this function.
15

Discuss the continuity of the function at the point x = 0.
16

Discuss the continuity of the function at the point x = 1/2.
17

Discuss the continuity of at x = 0.
18

For what value of k is the function continuous at
x = 1?
19

Determine the value of the constant k so that the function is continuous at x = 1.
20

For what value of k is the function continuous at
x = 0?
21

Determine the value of the constant k so that the function is continuous at x = 2.
22

Determine the value of the constant k so that the function is continuous at x = 0.
23

Find the values of a so that the function is continuous at x = 2.
24

Prove that the function remains discontinuous at x = 0, regardless of the choice of k.
25

Find the value of k if f(x) is continuous at x = π/2, where

26

Determine the values of a, b, c for which the function is continuous at x = 0.
27

If is continuous at x = 0, find k.
28

If is continuous at x = 4, find a, b.
29

For what value of k is the function continuous at x = 0?
30

Let x ≠ 0. Find the value of f at x = 0 so that f becomes continuous at x = 0.
31

If is continuous at x = 2, find k.
32

If is continuous at x = 0, find k.
33

Extend the definition of the following by continuity at the point x = π.
34

If is continuous at x = 0, then find f(0).
35

Find the value of k for which is continuous at x = 0.
36

In each of the following, find the value of the constant k so that the given function is continuous at the indicated point :

at x = 0
36

In each of the following, find the value of the constant k so that the given function is continuous at the indicated point :

at x = 1
36

In each of the following, find the value of the constant k so that the given function is continuous at the indicated point :

at x = 0
36

In each of the following, find the value of the constant k so that the given function is continuous at the indicated point :

at x = 5
36

In each of the following, find the value of the constant k so that the given function is continuous at the indicated point :

at x = 5
36

In each of the following, find the value of the constant k so that the given function is continuous at the indicated point :

at x = 1
36

In each of the following, find the value of the constant k so that the given function is continuous at the indicated point :

at x = 0
36

In each of the following, find the value of the constant k so that the given function is continuous at the indicated point :

at x = 2.
37

Find the values of a and b so that the function f given by is continuous at x = 3 and x = 5
38

If Show that f is continuous at x = 1.
39

Discuss the continuity of the f(x) at the indicated points :

f(x) = |x| + |x – 1| at x = 0, 1.
39

Discuss the continuity of the f(x) at the indicated points :

f(x) = |x – 1| + |x + 1| at x = – 1, 1.
40

Prove that is discontinuous at

x = 0.
41

If then what should be the value of k so that f(x) is continuous at x = 0.
42

For what value of is the function continuous at x = 0? What about continuity at x = ± 1?
43

For what value of k is the following function continuous at x = 2?
44

Let . If f(x) is continuous at
 find a and b.
45

If the function f(x), defined below is continuous at x = 0, find the value of k:
46

Find the relationship between ‘a’ and ‘b’ so that the function ‘f’ defined by is continuous at x = 3.