Book: RD Sharma - Mathematics (Volume 1)
Chapter: 9. Continuity
Subject: Maths - Class 12th
Q. No. 26 of Exercise 9.1
Listen NCERT Audio Books - Kitabein Ab Bolengi
26
Determine the values of a, b, c for which the function 
is continuous at x = 0.
Given:
f(x) is continuous at x = 0
For f(x) to be continuous at x = 0,f(0)– = f(0) + = f(0)
LHL = f(0)– = 
1
(a + 1) + 1
(a + 1) + 1
f(0)–
a + 2 ...... (1)
RHL = f(0 + ) = 
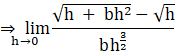
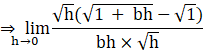
Take the complex conjugate of
,
i.e,
and multiply it with numerator and denominator.
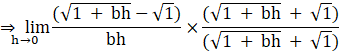
(a + b)(a–b) = a2– b2
f(0) + 
...... (2)
since, f(x) is continuous at x = 0,From (1) & (2),we get,
a + 2 = 
a = 
–2
a = 
Also,
f(0)– = f(0) + = f(0)
f(0) = c
c = a + 2 = 
c = 
So the values of a = 
,c = 
and b = R–{o}(any real number except 0 )
26
