Let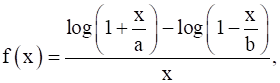 
x ≠ 0. Find the value of f at x = 0 so that f becomes continuous at x = 0.
For f(x) to be continuous at x = 0, f(0)–= f(0) + =f(0)
LHL = f(0)– = 
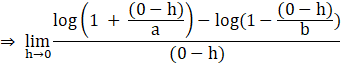
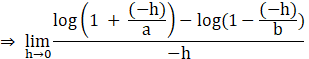
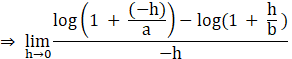
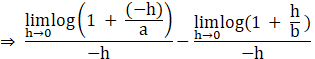
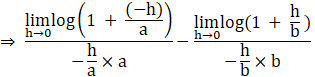
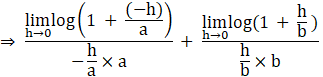
hence,f(0) = 
30
Let 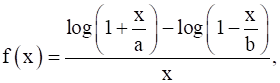x ≠ 0. Find the value of f at x = 0 so that f becomes continuous at x = 0.
For f(x) to be continuous at x = 0, f(0)–= f(0) + =f(0)
LHL = f(0)– =
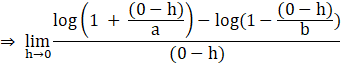
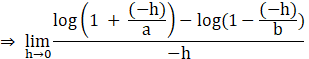
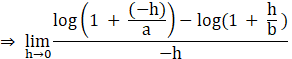
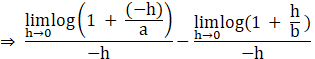
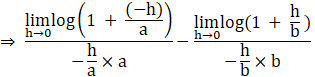
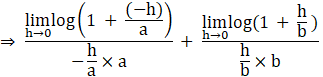
hence,f(0) =