In each of the following, find the value of the constant k so that the given function is continuous at the indicated point :
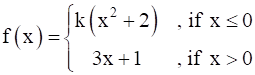 at x = 0
at x = 0
Given:
f(x) is continuous at x = 0
If f(x) to be continuous at x = 0,then,f(0)– = f(0) + = f(0)
LHL = f(0)– = ![]()
![]()
![]()
![]()
![]() k(0 + 2)
k(0 + 2)
![]() 2k ...(1)
2k ...(1)
RHL = f(0) + = ![]()
![]()
![]()
![]() 1 ...(2)
1 ...(2)
Since, f(x) is continuous at x = 0,From (1) & (2),we get,
2k = 1
![]() k =
k = ![]()
36