Find the values of a and b so that the function f given by 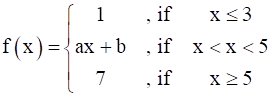 is continuous at x = 3 and x = 5
is continuous at x = 3 and x = 5
Given:
f(x) is continuous at x = 3 & x = 5
If f(x) to be continuous at x = 3,then,f(3)– = f(3) + = f(3)
LHL = f(3)– = ![]()
= 1 ...(1)
RHL = f(3) + = ![]()
![]()
⇒ a(3 + 0) + b
⇒ 3a + b ...(2)
Since ,f(x) is continuous at x = 3 and From (1) & (2),we get
3a + b = 1 ...(3)
Similarly ,f(x) is continuous at x = 5
If f(x) to be continuous at x = 5,then, f(5)– = f(5) + = f(5)
LHL = f(5)– = ![]()
![]()
⇒ a(5–0) + b
⇒ 5a + b ...(4)
RHL = f(5) + = ![]()
![]() 7 ...(5)
7 ...(5)
Since , f(x) is continuous at x = 5 and From (4) & (5),we get,
5a + b = 7 ...(6)
Now equate (3) & (6)
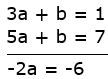
⇒ a = 3
Now Substitute a = 3 in any one of above equation(3) & (6) ,
3a + b = 1
⇒ 3(3) + b = 1
⇒ 9 + b = 1
⇒ b = –8
37