Let 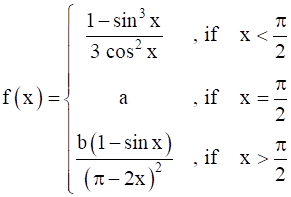 . If f(x) is continuous at
. If f(x) is continuous at![]() find a and b.
find a and b.
Given:
f(x) is continuous at x = ![]() & f(
& f(![]() ) = a,
) = a,
If f(x) to be continuous at x = ![]() ,we have to show, f(
,we have to show, f(![]() )– = f(
)– = f(![]() ) + = f(
) + = f(![]() )
)
LHL = f(![]() )– =
)– = ![]()
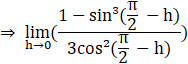
![]() sin(
sin(![]() –x) = cosx
–x) = cosx
![]() cos(
cos(![]() –x) = sinx
–x) = sinx
![]()
![]()
![]()
![]() (a3–b3) = (a–b)(a2 + ab + b2)
(a3–b3) = (a–b)(a2 + ab + b2)
![]()
![]()
![]()
![]()
∴ cos(0) = 1
![]()
![]()
![]() ...(1)
...(1)
LHL = f(![]() ) + =
) + =![]()
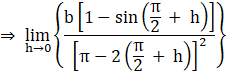
![]()
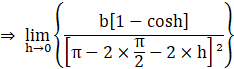
![]()
![]()
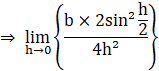
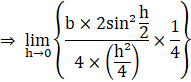
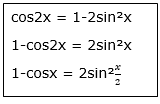
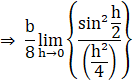
![]() 1
1
![]() ...(2)
...(2)
f(x) is continuous at x = ![]() & f(
& f(![]() ) = a ,and from (1) & (2),we get
) = a ,and from (1) & (2),we get
f(![]() )– = f(
)– = f(![]() ) + = f(
) + = f(![]() )
)
![]() = a
= a
![]() a =
a = ![]()
![]()
⇒ b = 4
Hence ,a = ![]() & b = 4
& b = 4
44