RD Sharma - Mathematics (Volume 1)

Book: RD Sharma - Mathematics (Volume 1)

Chapter: 9. Continuity

Subject: Maths - Class 12th

Q. No. 46 of Exercise 9.1

Listen NCERT Audio Books to boost your productivity and retention power by 2X.

46

Find the relationship between ‘a’ and ‘b’ so that the function ‘f’ defined by 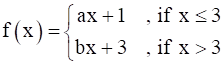is continuous at x = 3.

we have to find the value of 'a' & 'b'


Given:


f(x) is continuous at x = 3


If f(x) is be continuous at x = 3,then,f(3)– = f(3) + = f(3)


LHL = f(3)– =




⇒ 3a – 0 × a + 1


⇒ 3a + 1 .....(1)


LHL = f(3) + =




⇒ 3b – 0 × b + 3


⇒ 3b + 3 ...(2)


Since ,f(x) is continuous at x = 3 and From (1) & (2),we get


3a + 1 = 3b + 3


⇒ 3a + 3b = 3 – 1


⇒ 3a + 3b = 2


⇒ 3(a + b) = 2


⇒ (a + b) =


Chapter Exercises

Exercise 9.1
Exercise 9.2
Very short answer
MCQ

More Exercise Questions

1

Test the continuity of the following function at the origin :
2

A function f(x) is defined as Show that f(x) is continuous at x = 3.
3

A function f(x) is defined as

Show that f(x) is continuous at x = 3.
4

If Find whether f(x) is continuous at x = 1.
5

If Find whether f(x) is continuous at x = 0.
6

If Find whether f is continuous at x = 0.
7

Let Show that f(x) is discontinuous at x = 0.
8

Show that is discontinuous at x = 0.
9

Show that is discontinuous at x = a.
10

Discuss the continuity of the following functions at the indicated point(s).

at x = 0
10

Discuss the continuity of the following functions at the indicated point(s).

at x = 0
10

Discuss the continuity of the following functions at the indicated point(s).

at
x = a
10

Discuss the continuity of the following functions at the indicated point(s).

at x = 0
10

Discuss the continuity of the following functions at the indicated point(s).

at x = 1
10

Discuss the continuity of the following functions at the indicated point(s).

at x = 1
10

Discuss the continuity of the following functions at the indicated point(s).

at x = 0
10

Discuss the continuity of the following functions at the indicated point(s).

at x = a
11

Show that is discontinuous at x = 1.
12

Show that is continuous at x = 0
13

Find the value of ‘a’ for which the function f defined by is continuous at x = 0.
14

Examine the continuity of the function at x = 0. Also sketch the graph of this function.
15

Discuss the continuity of the function at the point x = 0.
16

Discuss the continuity of the function at the point x = 1/2.
17

Discuss the continuity of at x = 0.
18

For what value of k is the function continuous at
x = 1?
19

Determine the value of the constant k so that the function is continuous at x = 1.
20

For what value of k is the function continuous at
x = 0?
21

Determine the value of the constant k so that the function is continuous at x = 2.
22

Determine the value of the constant k so that the function is continuous at x = 0.
23

Find the values of a so that the function is continuous at x = 2.
24

Prove that the function remains discontinuous at x = 0, regardless of the choice of k.
25

Find the value of k if f(x) is continuous at x = π/2, where

26

Determine the values of a, b, c for which the function is continuous at x = 0.
27

If is continuous at x = 0, find k.
28

If is continuous at x = 4, find a, b.
29

For what value of k is the function continuous at x = 0?
30

Let x ≠ 0. Find the value of f at x = 0 so that f becomes continuous at x = 0.
31

If is continuous at x = 2, find k.
32

If is continuous at x = 0, find k.
33

Extend the definition of the following by continuity at the point x = π.
34

If is continuous at x = 0, then find f(0).
35

Find the value of k for which is continuous at x = 0.
36

In each of the following, find the value of the constant k so that the given function is continuous at the indicated point :

at x = 0
36

In each of the following, find the value of the constant k so that the given function is continuous at the indicated point :

at x = 1
36

In each of the following, find the value of the constant k so that the given function is continuous at the indicated point :

at x = 0
36

In each of the following, find the value of the constant k so that the given function is continuous at the indicated point :

at x = 5
36

In each of the following, find the value of the constant k so that the given function is continuous at the indicated point :

at x = 5
36

In each of the following, find the value of the constant k so that the given function is continuous at the indicated point :

at x = 1
36

In each of the following, find the value of the constant k so that the given function is continuous at the indicated point :

at x = 0
36

In each of the following, find the value of the constant k so that the given function is continuous at the indicated point :

at x = 2.
37

Find the values of a and b so that the function f given by is continuous at x = 3 and x = 5
38

If Show that f is continuous at x = 1.
39

Discuss the continuity of the f(x) at the indicated points :

f(x) = |x| + |x – 1| at x = 0, 1.
39

Discuss the continuity of the f(x) at the indicated points :

f(x) = |x – 1| + |x + 1| at x = – 1, 1.
40

Prove that is discontinuous at

x = 0.
41

If then what should be the value of k so that f(x) is continuous at x = 0.
42

For what value of is the function continuous at x = 0? What about continuity at x = ± 1?
43

For what value of k is the following function continuous at x = 2?
44

Let . If f(x) is continuous at
 find a and b.
45

If the function f(x), defined below is continuous at x = 0, find the value of k:
46

Find the relationship between ‘a’ and ‘b’ so that the function ‘f’ defined by is continuous at x = 3.

Students Store