Prove that the function 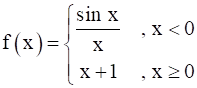 is everywhere continuous.
is everywhere continuous.
A real function f is said to be continuous at x = c, where c is any point in the domain of f if :
![]() where h is a very small ‘+ve’ no.
where h is a very small ‘+ve’ no.
i.e. left hand limit as x → c (LHL) = right hand limit as x → c (RHL) = value of function at x = c.
This is very precise, using our fundamental idea of the limit from class 11 we can summarise it as
A function is continuous at x = c if :
![]()
Here we have,
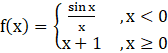 …….equation 1
…….equation 1
To prove it everywhere continuous we need to show that at every point in the domain of f(x) [ domain is nothing but a set of real numbers for which function is defined ]
![]()
Clearly from definition of f(x) {see from equation 1}, f(x) is defined for all real numbers.
∴ we need to check continuity for all real numbers.
Let c is any random number such that c < 0 [thus c being a random number, it can include all negative numbers ]
f(c) = ![]() [ using eqn 1]
[ using eqn 1]
![]()
Clearly, ![]()
∴ We can say that f(x) is continuous for all x < 0
Now, let m be any random number from the domain of f such that m > 0
thus m being a random number, it can include all positive numbers]
f(m) = m+1 [using eqn 1]
![]()
Clearly, ![]()
∴ We can say that f(x) is continuous for all x > 0
As zero is a point at which function is changing its nature so we need to check LHL, RHL separately
f(0) = 0+1 = 1 [using eqn 1]
LHL = ![]()
[∵ sin – θ = – sin θ and ![]() ]
]
RHL = ![]()
Thus LHL = RHL = f(0).
∴ f(x) is continuous at x = 0
Hence, we proved that f is continuous for x < 0 ; x > 0 and x = 0
Thus f(x) is continuous everywhere.
Hence, proved.