Find the points of discontinuity, if any, of the following functions :
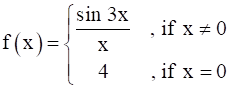
Basic Idea:
A real function f is said to be continuous at x = c, where c is any point in the domain of f if :
![]() where h is a very small ‘+ve’ no.
where h is a very small ‘+ve’ no.
i.e. left hand limit as x → c (LHL) = right hand limit as x → c (RHL) = value of function at x = c.
This is very precise, using our fundamental idea of limit from class 11 we can summarise it as, A function is continuous at x = c if :
![]()
Here we have,
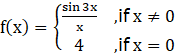 …Equation 1
…Equation 1
The function is defined for all real numbers, so we need to comment about its continuity for all numbers in its domain ( domain = set of numbers for which f is defined )
Let c is any random number such that c ≠ 0 [thus c being a random number, it can include all numbers except 0 ]
f(c) = ![]() [ using eqn 1]
[ using eqn 1]
![]()
Clearly, ![]()
∴ We can say that f(x) is continuous for all x ≠ 0
As zero is a point at which function is changing its nature, so we need to check the continuity here.
f(0) = 4 [using eqn 1]
LHL = ![]()
[∵ sin –θ = – sin θ and ![]() ]
]
RHL = ![]()
Thus LHL = RHL ≠ f(0)
∴ f(x) is discontinuous at x = 0
Hence, f is continuous for all x ≠ 0 but discontinuous at x = 0.