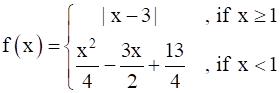
Basic Idea:

A real function f is said to be continuous at x = c, where c is any point in the domain of f if :

where h is a very small ‘+ve’ no.

i.e. left hand limit as x → c (LHL) = right hand limit as x → c (RHL) = value of function at x = c.

This is very precise, using our fundamental idea of limit from class 11 we can summarise it as, A function is continuous at x = c if :

NOTE: Idea of modulus function |x| : You can think this function as a machine in which you can give it any real no. as an input and it returns its absolute value i.e. if positive is entered it returns the same no and if negative is entered it returns the corresponding positive no.

Eg:– |2| = 2 ; |–2| = –(–2) = 2

Similarly, we can define it for variable x, if x ≥ 0 |x| = x

If x < 0 |x| = (–x)

∴

Here we have,

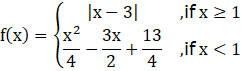
Applying the idea of mod function, f(x) can be rewritten as:

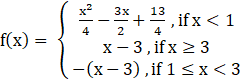……equation 1

Function is defined for all real numbers so we need to comment about its continuity for all numbers in its domain (domain = set of numbers for which f is defined )

Let c is any random number such that c < 1 [thus c being a random number, it can include all numbers less than 1]

f(c) = [ using eqn 1]

Clearly,

∴ We can say that f(x) is continuous for all x < 1

As x = 1 is a point at which function is changing its nature, so we need to check the continuity here.

f(1) = | 1 – 3 | = 2 [using eqn 1]

LHL =

RHL =

Thus LHL = RHL = f(1)

∴ f(x) is continuous at x = 1

Now, again f(x) is changing its nature at x = 3, so we need to check continuity at x = 3

f(3) = 3– 3 = 0 [using eqn 1]

LHL =

RHL =

Thus LHL = RHL = f(3)

∴ f(x) is continuous at x = 3

For x > 3 ; f(x) = x–3 whose plot is linear, so it is continuous for all x > 3

You can verify it by checking limits.

Similarly, for 1 < x < 3, f(x) = 3–x whose plot is again a straight line and thus continuous for all point in this range.

Hence, f(x) is continuous for all real x.