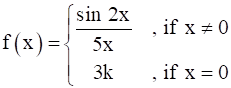
Basic Concept:

A real function f is said to be continuous at x = c, where c is any point in the domain of f if :

where h is a very small ‘+ve’ no.

i.e. left hand limit as x → c (LHL) = right hand limit as x → c (RHL) = value of function at x = c.

This is very precise, using our fundamental idea of limit from class 11 we can summarise it as, A function is continuous at x = c if :

Here we have,

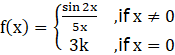Equation 1

Function is defined for all real numbers and we need to find the value of k so that it is continuous everywhere in its domain (domain = set of numbers for which f is defined)

As, for x ≠ 0 it is just a combination of trigonometric and linear polynomial both of which are continuous everywhere. It can be verified using limits and also by plotting curves. Since we are given that function is continuous everywhere so don’t need to bother about that.

As x = 0 is only point at which function is changing its nature so it needs to be continuous here.

f(0) = 3k [using eqn 1]

and,

[∵ ]

∵ f(x) is continuous everywhere [given in question]

∴ 3k =

∴ k =