The function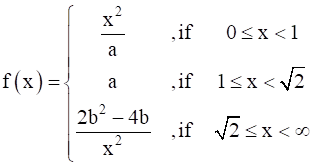 is continuous on [0, ∞]. Find the most suitable values of a and b.
is continuous on [0, ∞]. Find the most suitable values of a and b.
Basic Concept:
A real function f is said to be continuous at x = c, where c is any point in the domain of f if :
![]() where h is a very small ‘+ve’ no.
where h is a very small ‘+ve’ no.
i.e. left hand limit as x → c (LHL) = right hand limit as x → c (RHL) = value of function at x = c.
This is very precise, using our fundamental idea of limit from class 11 we can summarise it as, A function is continuous at x = c if :
![]()
Here we have,
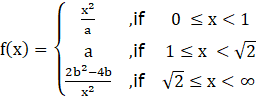 …………………..equation 1
…………………..equation 1
The function is defined for [0,∞] and we need to find the value of a and b so that it is continuous everywhere in its domain (domain = set of numbers for which f is defined)
To find the value of constants always try to check continuity at the values of x for which f(x) is changing its expression.
As most of the time discontinuities are here only, if we make the function continuous here, it will automatically become continuous everywhere
From equation 1 ,it is clear that f(x) is changing its expression at x = 1
Given,
f(x) is continuous everywhere
![]()
![]() [using basic ideas of limits and continuity]
[using basic ideas of limits and continuity]
![]() [considering LHL as LHL will give expression inclusive of a ]
[considering LHL as LHL will give expression inclusive of a ]
![]() [using equation 1]
[using equation 1]
∴ ![]()
∴ a = ± 1 …………… equation 2
Also from equation 1 ,it is clear that f(x) is also changing its expression at x = √2
Given,
f(x) is continuous everywhere
![]()
![]() [using basic ideas of limits and continuity]
[using basic ideas of limits and continuity]
![]() [considering LHL as LHL will give expression inclusive of a & b]
[considering LHL as LHL will give expression inclusive of a & b]
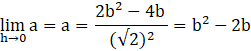
[using equation 1]
∴ b2 – 2b = a ……………….Equation 3
From equation 2, a = –1
b2 – 2b = –1
⇒ b2 – 2b + 1 = 0
⇒ (b – 1)2 = 0
∴ b = 1 when a = –1
Putting a = 1 in equation 3:
b2 – 2b = 1
⇒ b2 – 2b – 1 = 0
⇒ ![]()
Thus,
For a = –1 ; b = 1
For a = 1 ; b = 1 ± √2