Let 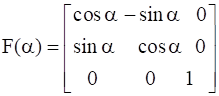 and
and 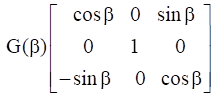 . Show that
. Show that
[G(β)] – 1 = G( – β)
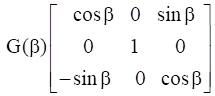
|G(β)| = ![]() = 1
= 1
Cofactors of A are:
C11 = cos β C21 = sin α C31 = sin β
C12 = 0 C22 = 1 C32 = 0
C13 = sin β C23 = 0 C33 = cos β
Adj G(β) = 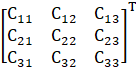
= 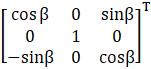
So, adj G(β) = 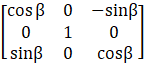 …… (i)
…… (i)
Now, [G(β)] – 1 = 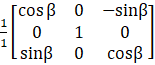
And, G( – β) = 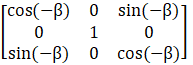
= 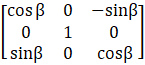
Hence, [G (β)] – 1 = G( – β)
16