Let 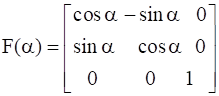 and
and 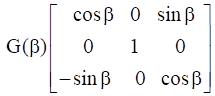 . Show that
. Show that
[F(α)G(β)] – 1 = G – ( – β) F( – α).
We have to show that
[F(α)G(β)] – 1 = G( – β) F( – α)
We have already shown that
[G (β)] – 1 = G( – β)
[F (α)] – 1 = F( – α)
And LHS = [F(α)G(β)] – 1
= [G (β)] – 1 [F (α)] – 1
= G( – β) F( – α)
Hence = RHS
16