Which of the following pairs of linear equations has unique solution, no solution or infinitely many solutions? In case there is a unique solution, find it by using cross multiplication method.
(i) x – 3y – 3 = 0
3x – 9y – 2 = 0
(ii) 2x + y = 5
3x + 2y = 8
(iii) 3x – 5y = 20
6x – 10y = 40
(iv) x – 3y – 7 = 0
3x – 3y – 15 = 0
(i) 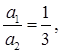
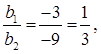
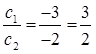
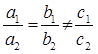
Therefore, the given sets of lines are parallel to each other. Therefore, they will not intersect each other and thus, there will not be any solution for these equations.
(ii) 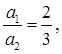
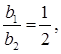
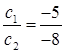
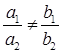
Therefore, they will intersect each other at a unique point and thus, there will be a unique solution for these equations.
By cross-multiplication method,

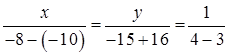
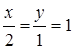
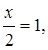
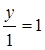
∴ x = 2, y = 1
(iii) 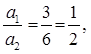
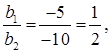
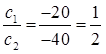
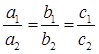
Therefore, the given sets of lines will be overlapping each other i.e., the lines will be coincident to each other and thus, there are infinite solutions possible for these equations.
(iv) 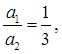
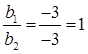

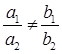
Therefore, they will intersect each other at a unique point and thus, there will be a unique solution for these equations.
By cross-multiplication,
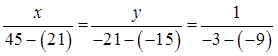
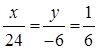

x = 4 and y = -1
∴ x = 4, y = -1