(i) 2x + 3y - 7 =0

(a - b)x + (a + b)y - (3a + b - 2) = 0

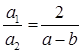
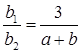
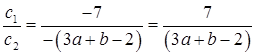
For infinitely many solutions,

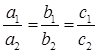
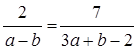
6a + 2b - 4 = 7a – 7b

a – 9b = -4.............. (i)

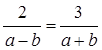
2a + 2b = 3a – 3b

a – 5b = 0...............(ii)

Subtracting (i) from (ii), we obtain

4b = 4

b = 1

Substituting this in equation (ii), we obtain

a - 5 × 1 = 0

a = 5

Hence, a = 5 and b = 1 are the values for which the given equations give infinitely many solutions.