Determine the equations of the line passing through the point (1, 2, –4) and perpendicular to the two lines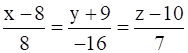 
and 
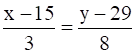
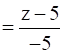
The Cartesian equation of a line passing through a point (x1, y1, z1) and having directional ratios proportional to a,b,c is given by,
The required line passes through the point (1,2,–4), now we need to find the direction ratios of the line which are a,b,c . this equation of the required line is,
It is given that a line having Cartesian equation 
is perpendicular to the required line, so the dot product equation will be equal to zero.
a×8 + b×(–16) + c×7 = 0
8a–16b+7c = 0 ……(i).
It is given that a line having Cartesian equation 
is perpendicular to the required line,
So the dot product equation will be equal to zero.
a×3 + b×8 + c×(–5) = 0
3a+8b–5c = 0 ……..(ii).
By solving equation (i) and (ii), we get, by using cross multiplication method,
= λ
a = 24λ, b = 61λ, c = 112λ
Put these values in the required equation of line,
Therefore, this is the required equation of line.