Let A, B and C be three point with position vector and

Thus,

As we know that cross product of two vectors gives a perpendicular vector so

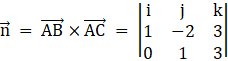
So, the equation of the required plane is

Also we have to find the coordinates of the point of intersection of this plane and the line

Any point on the line is of the form, p(3 + 2, – 1 – 2, – 1 + )

Point p(3 + 2, – 1 – 2, – 1 + ) lies in the plane,

so,

9(3 + 2) – 3(– 1 – 2) – (– 1 + ) = 14

27 + 18 – 3 – 6 + 1 – = 14

11 = – 11

= – 1

Thus the required point of intersection is

p(3 + 2, – 1 – 2, – 1 + )

put value of in this equation

p[3 + 2(– 1), – 1 – 2(– 1), – 1 + (– 1)]

p(1, 1, – 2)