Idea of parametric form of differentiation:

If y = f (θ) and x = g(θ) i.e. y is a function of θ and x is also some other function of θ.

Then dy/dθ = f’(θ) and dx/dθ = g’(θ)

We can write :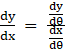

Given,

x = a cos θ ……equation 1

y = b sin θ ……equation 2

to prove : .

We notice a second order derivative in the expression to be proved so first take the step to find the second order derivative.

Let’s find

As

So, lets first find dy/dx using parametric form and differentiate it again.

…..equation 3

Similarly, ……equation 4

[∵

Differentiating again w.r.t x :

…..equation 5

[ using chain rule and ]

From equation 3:

∴

Putting the value in equation 5 :

From equation 1:

y = b sin θ

∴ …..proved.