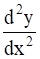Idea of parametric form of differentiation:

If y = f (θ) and x = g(θ) i.e. y is a function of θ and x is also some other function of θ.

Then dy/dθ = f’(θ) and dx/dθ = g’(θ)

We can write :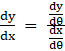

Given,

x = a (θ – sin θ) ……equation 1

y = a (1+ cos θ) ……equation 2

to find :

As,

So, lets first find dy/dx using parametric form and differentiate it again.

…..equation 3

Similarly,

……equation 4

[∵

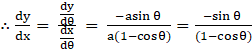…..equation 5

Differentiating again w.r.t x :

Using product rule and chain rule of differentiation together:

Apply chain rule to determine

[using equation 3]

[ ∵ ]

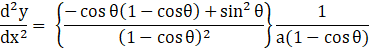
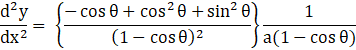
[ ∵1– cos θ = 2sin² θ/2]

∴