Note: y₂ represents second order derivative i.e. and y₁ = dy/dx

Given,

y = (sin^–1 x)² ……equation 1

to prove : (1–x²) y₂–xy₁–2=0

We notice a second order derivative in the expression to be proved so first take the step to find the second order derivative.

Let’s find

As,

So, lets first find dy/dx

Using chain rule we will differentiate the above expression

Let t = sin^–1 x => [using formula for derivative of sin^–1x]

And y = t²

…….equation 2

Again differentiating with respect to x applying product rule:

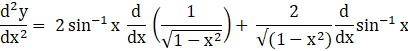
[using ]

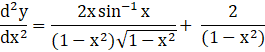
Using equation 2 :

∴ (1–x²) y₂–xy₁–2=0 ……proved