Given: a ladder 13 m long leans against a wall. The foot of the ladder is pulled along the ground away from the wall, at the rate of 1.5m/sec

To find how fast is the angle θ between the ladder and the ground is changing when the foot of the ladder is 12 m away from the wall

Let AC be the position of the ladder initially, then AC = 13m.

DE be the position of the ladder after being pulled at the rate of 1.5m/sec, then DE = 13m as shown in the below figure.

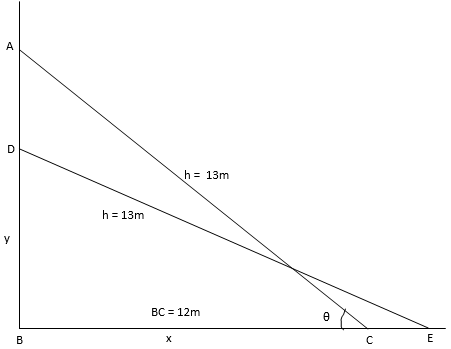
So it is given that foot of the ladder is pulled along the ground away from the wall, at the rate of 1.5m/sec

……………(i)

Consider ΔABC, it is right angled triangle, so by applying the Pythagoras theorem, we get

AB² + BC² = AC²

⇒ y² + x² = h²……….(ii)

⇒ y² + (12)² = (13)²

⇒ y² = 169 - 144 = 25

⇒ y = 5

And in same triangle,

Now differentiate equation(ii) with respect to time, we get

Now substituting the values of x, y, h and (from equation(i)), we get

The value of h is always constant as the ladder is not increasing or decreasing in size, hence the above equation becomes,

And considering the same triangle,

Differentiating the above equation with respect to time we get

[applying quotient rule ]

Substituting the values of (from equation(iii)), x, y, (from equation(iv) and (from equation(i)) the above equation becomes,

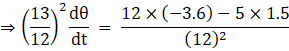
Hence the angle θ between the ladder and the ground is changing at the rate of - 0.3 rad/sec when the foot of the ladder is 12 m away from the wall.