Given: a balloon in the form of a right circular cone surmounted by a hemisphere, having a diameter equal to the height of the cone, is being inflated

To find: how fast is its volume changing with respect to its total height h, when h = 9 cm

Solution:

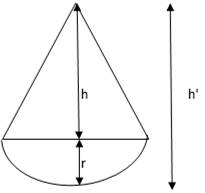
Let height of the cone be h’

And the radius of the hemisphere be r

As per the given criteria,

Let the total height of the balloon be h

Then

…………(i)

So,

Volume of the balloon (V) = Volume of the cone + Volume of the hemisphere

This is the volume of the balloon

Now will substitute the value of h’ from equation (i), we get

Now differentiate the above equation with respect to h, we get

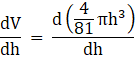
When h = 9cm, we get

Hence at the rate of 12 cm² the volume changes with respect to its total height.