Sand is being poured onto a conical pile at the constant rate of 50 cm 3 /minute such that the height of the cone is always one half of the radius of its base. How fast is the height of the pile increasing when the sand is 5 cm deep?

Question

Philoid · Accepted Answer

Let the volume be V, height be h and radius be r of the cone at any instant of time.

We know, volume of the cone is

And its given height of the cone is always one half of the radius of its base, i.e.,

So the new volume becomes

Differentiate the above equation with respect to time, we get

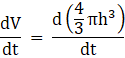
And it is also given that the sand is being poured onto a conical pile at the constant rate of 50 cm³/minute, so , so the above equation becomes,

Now when height of the pile is 5cm, the above equation becomes

Therefore, the rate of height of the pile increasing when the sand is 5 cm deep is cm/min.

Sand is being poured onto a conical pile at the constant rate of 50 cm3/minute such that the height of the cone is always one half of the radius of its base. How fast is the height of the pile increasing when the sand is 5 cm deep?

Sand is being poured onto a conical pile at the constant rate of 50 cm³/minute such that the height of the cone is always one half of the radius of its base. How fast is the height of the pile increasing when the sand is 5 cm deep?