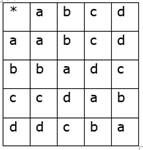
We observe the following:

a * b = b * a = b

c * a = a * c = c

a * d = d * a = d

b * c = c * b = d

b * d = d * b = c

c * d = d * c = b

There ‘ * ’ is commutative.

Also,

a * (b * c) = a * (d) = d (From above)

(a * b) * c = (b) * c = d (Also from above)

Hence, ‘ * ’ is associative too.

Therefore, to find the identity element, e for e belong to S, we need:

a * e = e * a = a, a belong to S.

Therefore, a * e = a

e = a (since, a * a = a, from the given table)

To find out the inverse, a * x = e = b * x, x belongs to S

a * x = e

x = a (From the given table)

Therefore, the inverse of a is a, b is b, c is c and d is d.