RD Sharma - Mathematics (Volume 1)

Book: RD Sharma - Mathematics (Volume 1)

Chapter: 17. Increasing and Decreasing Functions

Subject: Maths - Class 12th

Q. No. 1 of Exercise 17.2

Listen NCERT Audio Books to boost your productivity and retention power by 2X.

1

Find the intervals in which the following functions are increasing or decreasing.

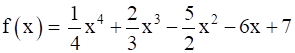
Given:- Function


Theorem:- Let f be a differentiable real function defined on an open interval (a,b).


(i) If f’(x) > 0 for all , then f(x) is increasing on (a, b)


(ii) If f’(x) < 0 for all , then f(x) is decreasing on (a, b)


Algorithm:-


(i) Obtain the function and put it equal to f(x)


(ii) Find f’(x)


(iii) Put f’(x) > 0 and solve this inequation.


For the value of x obtained in (ii) f(x) is increasing and for remaining points in its domain it is decreasing.


Here we have,



⇒


⇒ f’(x) = x3 + 2x2 – 5x – 6


For f(x) lets find critical point, we must have


⇒ f’(x) = 0


⇒ x3 + 2x2 – 5x – 6 = 0


⇒ (x+1)(x – 2)(x + 3) = 0


⇒ x = –1, 2 , –3





clearly, f’(x) > 0 if –3 < x < –1 and x > 2


and f’(x) < 0 if x < –3 and –3 < x < –1


Thus, f(x) increases on (–3, –1) ∪ (2, ∞)


and f(x) is decreasing on interval (∞, –3) ∪ (–1, 2)



Chapter Exercises

Exercise 17.1
Exercise 17.2
MCQ

More Exercise Questions

1

Find the intervals in which the following functions are increasing or decreasing.

f(x) = 10 – 6x – 2x2
1

Find the intervals in which the following functions are increasing or decreasing.

f(x) = x2 + 2x – 5
1

Find the intervals in which the following functions are increasing or decreasing.

f(x) = 6 – 9x – x2
1

Find the intervals in which the following functions are increasing or decreasing.

f(x) = 2x3 – 12x2 + 18x + 15
1

Find the intervals in which the following functions are increasing or decreasing.

f(x) = 5 + 36x + 3x2 – 2x3
1

Find the intervals in which the following functions are increasing or decreasing.

f(x) = 8 + 36x + 3x2 – 2x3
1

Find the intervals in which the following functions are increasing or decreasing.

f(x) = 5x3 – 15x2 – 120x + 3
1

Find the intervals in which the following functions are increasing or decreasing.

f(x) = x3 – 6x2 – 36x + 2
1

Find the intervals in which the following functions are increasing or decreasing.

f(x) = 2x3 – 15x2 + 36x + 1
1

Find the intervals in which the following functions are increasing or decreasing.

f(x) = 2x3 + 9x2 + 12x + 20
1

Find the intervals in which the following functions are increasing or decreasing.

f(x) = 2x3 – 9x2 + 12x – 5
1

Find the intervals in which the following functions are increasing or decreasing.

f(x) = 6 + 12x + 3x2 – 2x3
1

Find the intervals in which the following functions are increasing or decreasing.

f(x) = 2x3 – 24x + 107
1

Find the intervals in which the following functions are increasing or decreasing.

f(x) = – 2x3 – 9x2 – 12x + 1
1

Find the intervals in which the following functions are increasing or decreasing.

f(x) = (x – 1) (x – 2)2
1

Find the intervals in which the following functions are increasing or decreasing.

f(x) = x3 – 12x2 + 36x + 17
1

Find the intervals in which the following functions are increasing or decreasing.

f(x) = 2x3 – 24x + 7
1

Find the intervals in which the following functions are increasing or decreasing.
1

Find the intervals in which the following functions are increasing or decreasing.

f(x) = x4 – 4x
1

Find the intervals in which the following functions are increasing or decreasing.
1

Find the intervals in which the following functions are increasing or decreasing.

f(x) = x4 – 4x3 + 4x2 + 15
1

Find the intervals in which the following functions are increasing or decreasing.
1

Find the intervals in which the following functions are increasing or decreasing.

f(x) = x8 + 6x2
1

Find the intervals in which the following functions are increasing or decreasing.

f(x) = x3 – 6x2 + 9x + 15
1

Find the intervals in which the following functions are increasing or decreasing.

f(x) = {x (x – 2)}2
1

Find the intervals in which the following functions are increasing or decreasing.

f(x) = 3x4 – 4x3 – 12x2 + 5
1

Find the intervals in which the following functions are increasing or decreasing.
1

Find the intervals in which the following functions are increasing or decreasing.
2

Determine the values of x for which the function f(x) = x2 – 6x + 9 is increasing or decreasing. Also, find the coordinates of the point on the curve y = x2 – 6x + 9 where the normal is parallel to the line
y = x + 5.
3

Find the intervals in which f(x) = sin x – cos x, where 0 < x < 2π is increasing or decreasing.
4

Show that f(x) = e2x is increasing on R.
5

Show that , x ≠ 0 is a decreasing function for all x ≠ 0.
6

Show that f(x) = loga x, 0 < a < 1 is a decreasing function for all x > 0.
7

Show that f(x) = sin x is increasing on (0, π/2) and decreasing on (π/2, π) and neither increasing nor decreasing in (0, π).
8

Show that f(x) = log sin x is increasing on (0, π/2) and decreasing on (π/2, π).
9

Show that f(x) = x – sin x is increasing for all x ϵ R.
10

Show that f(x) = x3 – 15x2 + 75x – 50 is an increasing function for all x ϵ R.
11

Show that f(x) = cos2 x is a decreasing function on (0, π/2).
12

Show that f(x) = sin x is an increasing function on (–π/2, π/2).
13

Show that f(x) = cos x is a decreasing function on (0, π), increasing in (–π, 0) and neither increasing nor decreasing in (–π, π).
14

Show that f(x) = tan x is an increasing function on (–π/2, π/2).
15

Show that f(x) = tan–1 (sin x + cos x) is a decreasing function on the interval (π/4, π /2).
16

Show that the function is decreasing on

17

Show that the function f(x) = cot–1 (sin x + cos x) is decreasing on (0, π/4) and increasing on (π/4, π/2).
18

Show that f(x) = (x – 1) ex + 1 is an increasing function for all x > 0.
19

Show that the function x2 – x + 1 is neither increasing nor decreasing on (0, 1).
20

Show that f(x) = x9 + 4x7 + 11 is an increasing function for all x ϵ R.
21

Prove that the function f(x) = x3 – 6x2 + 12x – 18 is increasing on R.
22

State when a function f(x) is said to be increasing on an interval [a, b]. Test whether the function f(x) = x2 – 6x + 3 is increasing on the interval [4, 6].
23

Show that f(x) = sin x – cos x is an increasing function on (–π /4, π /4)?
24

Show that f(x) = tan–1 x – x is a decreasing function on R ?
25

Determine whether f(x) = x/2 + sin x is increasing or decreasing on (–π /3, π/3) ?
26

Find the interval in which is increasing or decreasing ?
27

Find the intervals in which f(x) = (x + 2)e–x is increasing or decreasing ?
28

Show that the function f given by f(x) = 10x is increasing for all x ?
29

Prove that the function f given by f(x) = x – [x] is increasing in (0, 1) ?
30

Prove that the following function is increasing on r?

i. f(x) = 3x5 + 40x3 + 240x


ii. f(x) = 4x3 – 18x2 + 27x – 27
31

Prove that the function f given by f(x) = log cos x is strictly increasing on (–π/2, 0) and strictly decreasing on (0, π/2) ?
32

Prove that the function f given by f(x) = x3 – 3x2 + 4x is strictly increasing on R ?
33

33 Prove that the function f(x) = cos x is :

i. strictly decreasing on (0, π)


ii. strictly increasing in (π, 2π)


iii. neither increasing nor decreasing in (0, 2 π)
34

Show that f(x) = – x sin x is an increasing function on (0, π/2) ?
35

Find the value(s) of a for which f(x) = – ax is an increasing function on R ?
36

Find the values of b for which the function f(x) = sin x – bx + c is a decreasing function on R ?
37

Show that f(x) = x + cos x – a is an increasing function on R for all values of a ?
38

Let F defined on [0, 1] be twice differentiable such that | f”(x) ≤ 1 for all x ϵ [0, 1]. If f(0) = f(1), then show that |f’(x) | < 1 for all x ϵ [0, 1] ?
39

Find the intervals in which f(x) is increasing or decreasing :

i. f(x) = x |x|, x ϵ R


ii. f(x) = sin x + |sin x|, 0 < x ≤ 2 π


iii. f(x) = sin x (1 + cos x), 0 < x < π/2

Students Store