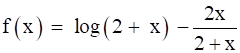
Given:- Function

Theorem:- Let f be a differentiable real function defined on an open interval (a,b).

(i) If f’(x) > 0 for all , then f(x) is increasing on (a, b)

(ii) If f’(x) < 0 for all , then f(x) is decreasing on (a, b)

Algorithm:-

(i) Obtain the function and put it equal to f(x)

(ii) Find f’(x)

(iii) Put f’(x) > 0 and solve this inequation.

For the value of x obtained in (ii) f(x) is increasing and for remaining points in its domain it is decreasing.

Here we have,

⇒

⇒

⇒

⇒

⇒

⇒

For f(x) to be increasing, we must have

⇒ f’(x) > 0

⇒

⇒ (x – 2) > 0

⇒ 2 < x < ∞

⇒ x ∈ (2, ∞)

Thus f(x) is increasing on interval (2, ∞)

Again, For f(x) to be decreasing, we must have

f’(x) < 0

⇒

⇒ (x – 2) < 0

⇒ –∞ < x < 2

⇒ x ∈ (–∞, 2)

Thus f(x) is decreasing on interval (–∞, 2)