Given: - Equations are: –

x – 4y – z = 11

2x – 5y + 2z = 39

– 3x + 2y + z = 1

Tip: - Theorem – Cramer’s Rule

Let there be a system of n simultaneous linear equations and with n unknown given by

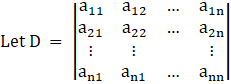
and let D_j be the determinant obtained from D after replacing the j^th column by

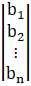
Then,

provided that D ≠ 0

Now, here we have

x – 4y – z = 11

2x – 5y + 2z = 39

– 3x + 2y + z = 1

So by comparing with theorem, lets find D , D₁ and D₂

Solving determinant, expanding along 1^st row

⇒ D = 1[( – 5)(1) – (2)(2)] + 4[(2)(1) + 6] – 1[4 + 5( – 3)]

⇒ D = 1[ – 5 – 4] + 4[8] – [ – 11]

⇒ D = – 9 + 32 + 11

⇒ D = 34

Again,

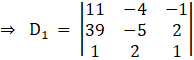
Solving determinant, expanding along 1^st row

⇒ D₁ = 11[( – 5)(1) – (2)(2)] + 4[(39)(1) – (2)(1)] – 1[2(39) – ( – 5)(1)]

⇒ D₁ = 11[ – 5 – 4] + 4[39 – 2] – 1[78 + 5]

⇒ D₁ = 11[ – 9] + 4(37) – 83

⇒ D₁ = – 99 – 148 – 45

⇒ D₁ = – 34

Again

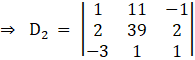
Solving determinant, expanding along 1^st row

⇒ D₂ = 1[39 – 2] – 11[2 + 6] – 1[2 + 117]

⇒ D₂ = 1[37] – 11(8) – 119

⇒ D₂ = – 170

And,

⇒

Solving determinant, expanding along 1^st row

⇒ D₃ = 1[ – 5 – (39)(2)] – ( – 4)[2 – (39)( – 3)] + 11[4 – ( – 5)( – 3)]

⇒ D₃ = 1[ – 5 – 78] + 4(2 + 117) + 11(4 – 15)

⇒ D₃ = – 83 + 4(119) + 11( – 11)

⇒ D₃ = 272

Thus by Cramer’s Rule, we have

⇒

⇒

⇒ x = – 1

again,

⇒

⇒

⇒ y = – 5

and,

⇒

⇒

⇒ z = 8