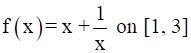
Lagrange’s mean value theorem states that if a function f(x) is continuous on a closed interval [a, b] and differentiable on the open interval (a, b), then there is at least one point x=c on this interval, such that

f(b)−f(a)=f′(c)(b−a)

This theorem is also known as First Mean Value Theorem.

∴ f(x) is continuous in [1, 3]

Differentiating with respect to x:

Here,

⇒ f’(x) exists for all values except 0

∴ f(x) is differentiable in (1, 3)

So both the necessary conditions of Lagrange’s mean value theorem is satisfied.

On differentiating with respect to x:

For f’(c), put the value of x=c in f’(x):

For f(3), put the value of x=3 in f(x):

For f(1), put the value of x=1 in f(x):

⇒ f(1) = 2

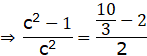
⇒ 6(c² – 1) = 4c²

⇒ 6c² – 6 = 4c²

⇒ 6c² – 4c² = 6

⇒ 2c² = 6

⇒ c² = 3

Hence, Lagrange’s mean value theorem is verified.