Lagrange’s mean value theorem states that if a function f(x) is continuous on a closed interval [a, b] and differentiable on the open interval (a, b), then there is at least one point x=c on this interval, such that

f(b)−f(a)=f′(c)(b−a)

This theorem is also known as First Mean Value Theorem.

f(x) = sin x – sin 2x – x on [0, π]

sin x and cos x functions are continuous everywhere on (−∞, ∞) and differentiable for all arguments.

So both the necessary conditions of Lagrange’s mean value theorem is satisfied.

f(x) = sin x – sin 2x – x

Differentiating with respect to x:

f(x) = sin x – sin 2x – x

For f’(c), put the value of x=c in f’(x):

f’(c) = cos c – 2cos 2c – 1

For f(π), put the value of x=π in f(x):

f(π) = sin π – sin 2π – π

= 0 – 0 – π

= – π

For f(0), put the value of x=0 in f(x):

f(0) = sin 0 – sin 2(0) – 0

= sin 0 – sin 0 – 0

= 0 – 0 – 0

= 0

⇒ cos c – 2cos 2c – 1 = – 1

⇒ cos c – 2(2cos² c – 1) = – 1 + 1

⇒ cos c – 4cos² c + 2 = 0

⇒ 4cos² c – cos c – 2 = 0

For quadratic equation, ax² + bx + c = 0

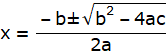
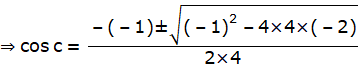
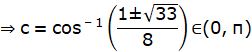
Hence, Lagrange’s mean value theorem is verified.