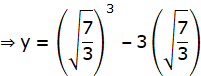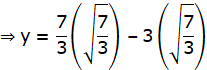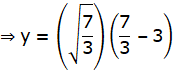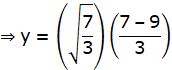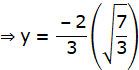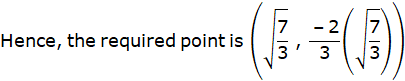Lagrange’s mean value theorem states that if a function f(x) is continuous on a closed interval [a, b] and differentiable on the open interval (a, b), then there is at least one point x=c on this interval, such that

f(b)−f(a)=f′(c)(b−a)

This theorem is also known as First Mean Value Theorem.

Let f(x) = x³ – 3x on [1, 2]

This interval [a, b] is obtained by x – coordinates of the points of the chord.

Every polynomial function is continuous everywhere on (−∞, ∞) and differentiable for all arguments.

Here, f(x) is a polynomial function. So it is continuous in [1, 2] and differentiable in (1, 2). So both the necessary conditions of Lagrange’s mean value theorem is satisfied.

f(x) = x³ – 3x

Differentiating with respect to x:

f’(x) = 3x² – 3

For f’(c), put the value of x=c in f’(x):

f’(c)= 3c² – 3

For f(2), put the value of x=2 in f(x):

f(2)= (2)³ – 3(2)

= 8 – 6

= 2

For f(1), put the value of x=1 in f(x):

f(1) = (1)³ – 3(1)

= 1 – 3

= – 2

f’(c) = f(2) – f(1)

⇒ 3c² – 3 = 2 – ( – 2)

⇒ 3c² – 3 = 2 + 2

⇒ 3c² = 4 + 3

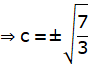
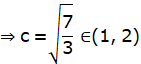
We know that, the value of c obtained in Lagrange’s Mean value Theorem is nothing but the value of x – coordinate of the point of the contact of the tangent to the curve which is parallel to the chord joining the points (1, – 2) and (2, 2).

Now, Put this value of x in f(x) to obtain y:

y = x³ – 3x