y = (sin 2x + cot x + 2)2 at x = π/2
Given:
y = (sin2x + cotx + 2)2at x = 
First, we have to find 
of given function, f(x),i.e, to find the derivative of f(x)
(xn) = n.xn – 1
The Slope of the tangent is 
⇒ y = (sin2x + cotx + 2)2
= 2
(sin2x + cotx + 2)2 – 1
(sin2x) + 
(cotx) + 
(2)}
= 2(sin2x + cotx + 2)
(cos2x)
+ ( – cosec2x) + (0)}
(sinx) = cosx
(cotx) = – cosec2x
⇒ 
= 2(sin2x + cotx + 2)(2cos2x – cosec2x)
Since, x = 
= 2
(sin2(
) + cot(
) + 2)(2cos2(
) – cosec2(
))
= 2
(sin(
) + cot(
) + 2)
(2cos(
) – cosec2(
))
= 2
(0 + 0 + 2)
(2( – 1) – 1)
sin(
) = 0, cos(
) = – 1
cot(
) = 0,cosec(
) = 1
⇒ 
= 2(2)
( – 2 – 1)
⇒ 
= 4
– 3
⇒ 
= – 12
The Slope of the tangent at x = 
is – 12
⇒ The Slope of the normal = 
⇒ The Slope of the normal =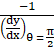 
⇒ The Slope of the normal = 
⇒ The Slope of the normal = 