Given:

The Slope of the tangent to the curve xy + ax + by = 2 at (1,1) is 2

First, we will find The Slope of tangent

we use product rule here,

(UV) = U + V

⇒ xy + ax + by = 2

⇒ x(y) + y(x) + a(x) + b(y) + = (2)

⇒ x + y + a + b = 0

⇒ (x + b) + y + a = 0

⇒ (x + b) = – (a + y)

⇒

since, The Slope of the tangent to the curve xy + ax + by = 2 at (1,1) is 2

i.e, = 2

⇒ {}_{(x = 1,y = 1)} = 2

⇒ = 2

⇒ – a – 1 = 2(1 + b)

⇒ – a – 1 = 2 + 2b

⇒ a + 2b = – 3 ...(1)

Also, the point (1,1) lies on the curve xy + ax + by = 2,we have

11 + a1 + b1 = 2

⇒ 1 + a + b = 2

⇒ a + b = 1 ...(2)

from (1) & (2),we get

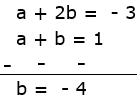
substitute b = – 4 in a + b = 1

a – 4 = 1

⇒ a = 5

So the value of a = 5 & b = – 4